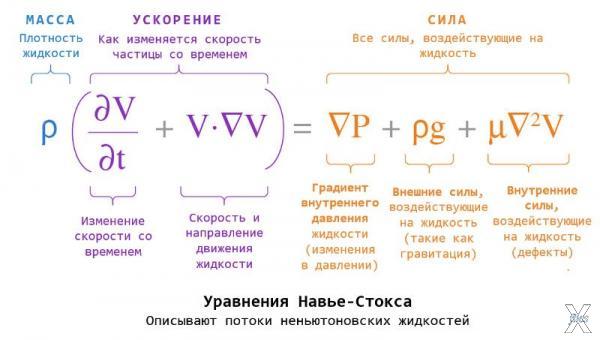
Уравнения Навье-Стокса описывают простой феномен, с которым мы сталкиваемся каждый день, к примеру, поток воды из крана, и несмотря на это, они являются задачкой буквально на миллион долларов. В физике существует уравнения, которые описывают все возможное: от растяжения пространства-времени до мельчайших колебаний фотонов. Но лишь одна система уравнений считается настолько сложной, что ее выбрали в качестве одной из семи “Задач тысячелетия”, за которые институт Клэя пообещал вознаграждение в $1 млн: уравнения Навье-Стокса...

Не так давно был получен новый результат, связанный с этой системой. Но если он что-то и дал, так это понимание, что добиться решения этой Задачи тысячелетия будет сложнее, чем ожидалось. Почему же эти уравнения, описывающий такой знакомый нам феномен как течение воды из крана, настолько сложнее описать математически, чем, скажем, уравнения Эйнштейна, описывающий такие умопромачительные объекты как черные дыры?

Оказывается, все дело в турбулентности. Это нечто, что мы все хоть раз испытали на себе, будь то в самолете, когда летели через зону нестабильного воздуха на высоте 10,000 км, или когда наблюдали, как закручивается воронка слива воды в ванной. Но привычность феномена не ведет к появлению знаний о нем: турбулентность — одна из самых непонятных вещей в физическом мире.


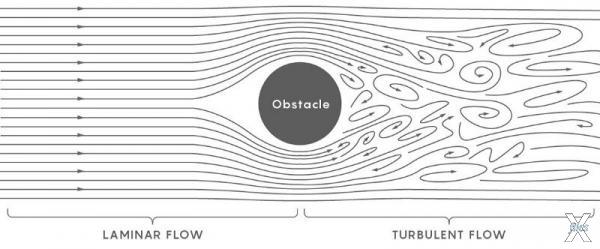
В качестве примера нетурбулентного течения можно назвать спокойную реку: каждая частица реки движется в одном направлении и с одной скоростью. Турбулентный поток возникает, когда река разбивается, и отдельные ее части начинают двигаться в разных направлениях с разными скоростями. Физики описывают образование турбулентности так: сначала появляется вихрь в спокойном потоке, а потом появляются вихри внутри этого вихря, а затем еще более мелкие вихри внутри тех вихрей, — сколько можете себе представить и больше. Таким образом поток получается разбит на мелкие потоки, взаимодействующие друг с другом, все двигающиеся в разных направлениях.

Ученые хотят понять, как именно спокойный поток, называемый ламинарным, разбивается в турбулентное течение, и научиться моделировать будущую форму жидкости, после того, как турбулентность вступит в свои права. Задача тысячелетия в этом плане более скромна: нужно лишь доказать, что решение всегда существует. То есть, могут ли эти уравнения описать любую жидкость, в любом начальном состоянии, на любой по длительности период в будущем?

“Первым шагом будет просто постараться доказать, что уравнения приводят к каким-то решениям,” — говорит Чарли Фефферман, математик из Принстонского университета. — “Конечно, так вы не поймете, как именно ведут себя жидкости, но если вы не знаете хотя бы это, вы не знаете ничего.”

Так как же доказать, что решения существуют? Что ж, нужно начать с размышления о том, что может заставить их не существовать. Система уравнений Навье-Стокса предполагает вычисление изменений таких переменных как скорость и давление. Математики беспокоятся о таком сценарии: вы вычисляете уравнения, и в какой-то конечный момент времени они говорят вам, что жидкость двигается бесконечно быстро. Это будет проблемой, потому что вы не можете вычислить изменения бесконечного значения также, как не можете разделить на ноль. Математики называют такой исход событий “аварийным” (blowup), в случае аварийного сценария уравнения нарушаются, и решений не существует.


Доказательство того, что авария не случится (и что решения всегда существуют) равносильно доказательству того, что максимальная скорость любой частицы жидкости всегда меньше какого-то конечного значения. Одной из самых важных переменных является кинетическая энергия внутри жидкости.

Когда вы начинаете моделировать поток, используя уравнения Навье Стокса, у вашей жидкости будет некое начальное количество энергии. Но в турбулентном потоке эта энергия может сконцентрироваться. Вместо того, чтобы быть распределенной по всей реке, кинетическая энергия может “собраться” в условно небольших вихрях, и частицы в этих вихрях (теоретически) могут ускориться до бесконечности.

“Чем сильнее я уменьшаю величины, тем меньше кинетическая энергия контролирует решение. Мое решение может делать все, что ему вздумается, и я не буду знать, как его контролировать,” — говорит Влад Викол, математик из Принстонского университета и соавтор новой статьи с Тристаном Бакмастером.

Математики классифицируют такие уравнения в частных производных как система Навье-Стокса по тому, насколько безумными они становятся на бесконечно малых значениях. Уравнения Навье-Стокса находятся на “безумном” конце этой градации. В некотором смысле, сложность математики этих уравнений является отражением той сложности турбулентных потоков, которые они должны суметь описать.

“Когда вы фокусирутесь на конкретном моменте, с математической точки зрения вы теряете всю информацию о решении,” — говорит Викол. — “Но турбулентность и должна такое описывать — перенос кинетической энергии от больших величин к всё меньшим и меньшим, оно буквально требует, чтобы вы сфокусировались.”


Когда вы говорите о математике уравнений физики, нет ничего необычного в том, чтобы задуматься: Изменит ли это то, как мы видим наш мир? В случае с уравнениями Навье-Стокса и Задачей тысячелетия ответ одновременно и да, и нет. После 200 лет экспериментов стало ясно, что уравнения работают: потоки, предсказанные Навье-Стоксом совпадают с теми, которые ученые наблюдают в экспериментах. Если вы физик, работающий в лаборатории, этого совпадения вам может быть достаточно. Но математики хотят большего — они хотят иметь возможность проверить, что мы можем следить, момент за моментом, как именно меняется поток (для любого начального состояния жидкости) и даже определить момент появления турбулентности.

“В поведении жидкостей много сюрпризов,” — говорит Фефферман. — “И эти сюрпризы объясняются фундаментальными уравнениями, которые говорят им, как нужно двигаться, но то, как перейти от уравнений, которые говорят, как им двигаться, к описанию того, как они на самом деле движутся, и по сей день остается тайной.”