Египтяне знали о Золотом Сечении за века до Фидия и Евклида, а о числах Фибоначчи за тысячи лет до рождения Фибоначчи. Мастера-Строители обучали своих учеников простым способам построения этих пропорций при помощи циркуля и угольника, о чем свидетельствуют мнемонические опоры, оставленные в виде канонов на стенах храмов. Странности и несоразмерности, введенные в ряд древних канонов, имели цель обратить внимание зрителя на универсальные законы и соотношения, которые предшествующие цивилизации считали Божественными и применяли при создании пирамид и храмов. Благодаря свойству масштабирования фрактальный ряд Серебряного Сечения впоследствии использовали и средневековые Мастера-Строители для проектирования частей зданий, а также арок, окон, входных проемов. Делая части здания соразмерными, архитектор превращал каждый его элемент в «обертон» - гармонику основного «тона» или размера, создавая «музыку в камне». Принцип Серебряного Сечения использовался суфийскими Мастерами при строительстве Альгамбры.

Трон Осириса

Ряд историков по-прежнему сомневается в том, что египтяне знали о Золотом Сечении за века до Фидия и Евклида, а о числах Фибоначчи за тысячи лет до рождения Фибоначчи. Бесспорные факты наличия Золотой Пропорции в древнеегипетских сооружениях ученые объясняют «случайными совпадениями» или интуитивно найденными соразмерностями.
Надеюсь, что расшифровка геометрических мемов Древнего Египта, ранее предложенных в качестве темы для размышления, поможет нам убедиться, что случайностей в применении египтянами Золотого Сечения и других сакральных соотношений быть не могло. Мастера-Строители обучали своих учеников простым способам построения этих пропорций при помощи циркуля и угольника, о чем свидетельствуют мнемонические опоры, оставленные в виде канонов на стенах храмов.


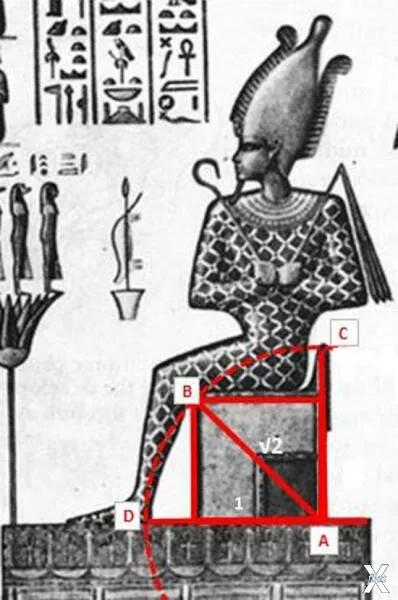
Первый рассмотренный нами канон представляет собой Осириса, сидящего на квадратном троне с непропорционально маленькой спинкой. Внутри квадрата зачем-то изображен малый квадрат, представляющий из себя четвертинку большого. Мы говорили о том, что странности и несоразмерности, введенные в ряд древних канонов, имели цель обратить внимание зрителя на универсальные законы и соотношения, которые предшествующие цивилизации считали Божественными и применяли при создании пирамид и храмов.
И сейчас мы увидим, что это были за законы.

Серебрянное сечение

Линия АВ – диагональ квадратного трона Осириса. Если поставить одну ножку циркуля в точку А, а другую – в точку В, и затем провести окружность, мы увидим, что окружность пройдет точно через точку С, которой оканчивается спинка трона. С другой стороны окружность пересечет точку D, как раз позади стоп Осириса. Итак, АВ = АС = АD.


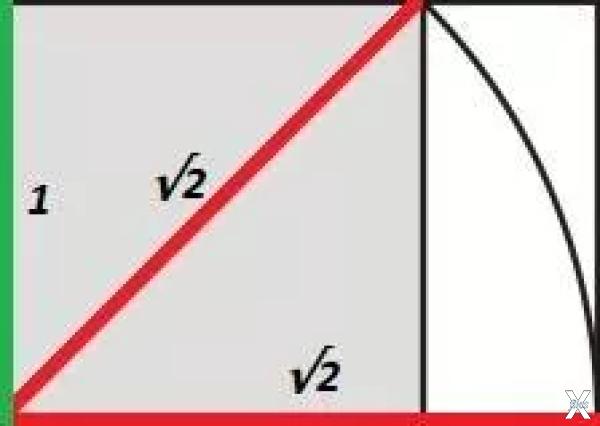
Если принять длину стороны квадрата трона за 1, то диагональ его по теореме Пифагора будет равна √2 (квадратному корню из двух). Каноном Трона Осириса египтяне запечатлели соотношение 1 : √2, с которого начинается так называемый ряд Серебряного Сечения.
Возможно, данный геометрический мем использовался при обучении учеников тому, как при помощи циркуля и угольника строится прямоугольник Серебряного Сечения.


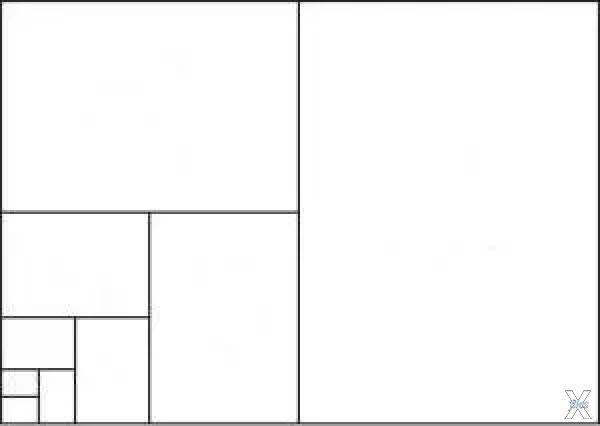
Чем уникален прямоугольник Серебряного Сечения, и почему Школы Строителей считали его столь важным? Дело в том, что прямоугольник со сторонами 1 : √2 обладает способностью создавать самоподобный (фрактальный) ряд, предоставляющий неограниченные возможности масштабирования.


Как мы обсуждали ранее в одной из заметок, листы формата стандартной серии А, которыми сейчас пользуется почти весь мир – А3, А4, А5 и т.д. – также имеют указанную пропорцию – 1 : √2. Из всех возможных соотношений данное сочетание было выбрано именно благодаря его фрактальности – способностью образовывать ряд самоподобных прямоугольников.
Универсальность пропорции 1 : √2 позволяла комбинировать размеры деталей объекта, при этом сохраняя их слаженность и гармоничность.


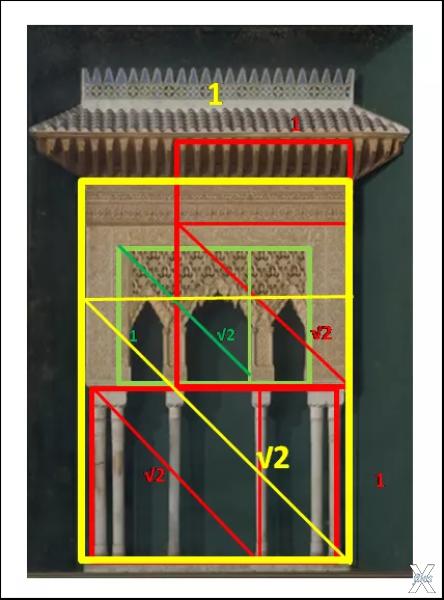
Благодаря свойству масштабирования фрактальный ряд Серебряного Сечения впоследствии использовали и средневековые Мастера-Строители для проектирования частей зданий, а также арок, окон, входных проемов. В качестве примера мы однажды рассматривали применение Серебряного Сечения суфийскими Мастерами-Строителями в архитектурной жемчужине Андалузии – несравненной Альгамбре:


Делая части здания соразмерными, архитектор превращал каждый его элемент в «обертон» – гармонику основного «тона» или размера, создавая «музыку в камне».


При всей значимости Серебряного Сечения, основным секретом древнеегипетского канона, названного нами «Троном Осириса», была все же другая, еще более важная пропорция.

Золотое сечение

Для тех уважаемых читателей, кто на этой странице недавно, напомним, что такое пропорция Золотого Сечения, и почему ее значение для всей жизни в нашей версии Вселенной столь велико.
Золотой Пропорцией (Ф) называется иррациональное число (1 + √5) ÷ 2, приблизительно равное 1,618, которое встречается в соотношении частей тела живых организмов, некоторых кристаллов, размеров небесных тел и элементарных частиц. Использование Золотой Пропорции – способ всего живого оставаться слаженным – и внутри себя, и во взаимодействии со всеми остальными. Благодаря этому «универсальному числу» Логоса, все сотворенное может делиться энергией и сосуществовать в гармонии, так как Золотая Пропорция – оптимальное соотношение, позволяющее вибрациям взаимодействовать конструктивно – усиливать друг друга, а не погашать. Поэтому волны (включая сердечные и мозговые ритмы, ритм дыхания) стремятся соотноситься с другими волнами в отношении Золотой Пропорции или ее производных. Рукотворные объекты, созданные с использованием Золотого Сечения, гармоничны не только эстетически, но и энергетически – в отношении использующих их людей, самой планеты и космоса за ее пределами. Благодаря этому они долговечны.
Наше иррациональное число 1,618 ни о чем не сказало бы древним египтянам, не использовавшим десятичных дробей, однако их Мастера прекрасно знали о сути Золотой Пропорции, а также о том, как создать ее геометрически при помощи циркуля и угольника.
Итак, вернемся к Трону Осириса.
Выше мы напомнили читателям, что Ф = (1 + √5) / 2 или 1 / 2 + √5 / 2.
Египтяне знали, что для построения Золотой Пропорции нужно вначале получить √5/2.
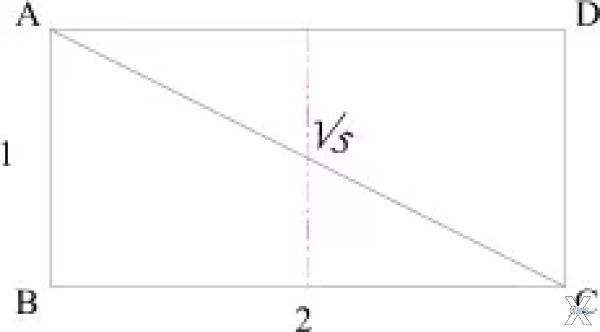
Геометрический смысл √5 – корня из пяти очень прост. Это – диагональ двух квадратов со стороной 1:


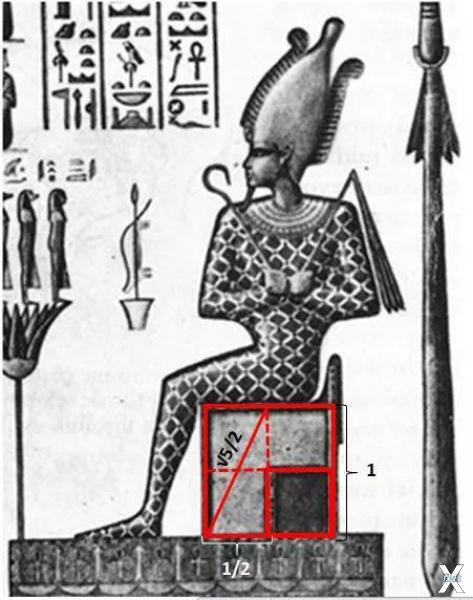
Следовательно, если взять два квадрата со стороной ½, их диагональ будет равна √5/2.
Мастер сакральной геометрии Роберт Лолор, из чьей книги взята иллюстрация с изображением Трона Осириса, первым обратил внимание на то, что сторона малого квадрата трона представляет собой половину стороны большого.


Это означает, что если принять сторону большого квадрата за единицу, сторона малого квадрата будет равна ½, а проведенная через два малых квадрата диагональ будет равна √5/2.
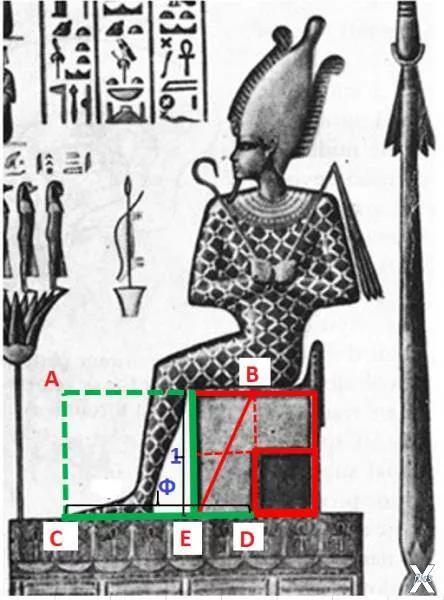
Теперь посмотрим на схему ниже.
Если поставить ножку циркуля в точку Е и провести окружность с радиусом ЕВ = √5/2, она коснется пола в точке С – как раз там, где начинаются ступни Осириса.
Мы знаем, что ЕD = ½ , СЕ = √5/2, следовательно, СD = Ф.
Сторона трона Осириса относится к СD как 1 : Ф – в пропорции Золотого Сечения. Прямоугольник АBCD является золотосеченным.


Возможно, учеников древнеегипетских Школ обучали построению Золотой Пропорции при помощи таких канонов. Мы точно знаем, что пропорция Ф применена при создании трех пирамид Гизы, а также храмов и святилищ, построенных вдоль Нила.
Об этом мы поговорим подробнее в следующей заметке, где расшифруем еще один геометрический канон (мем) древних египтян, запечатленный в образе набедренной повязки – шендита странной треугольной формы.