Как древний учёный ещё 2260 лет назад смог доказать, что Земля имеет форму шара и назвал её размеры
Сейчас практически каждому школьнику известно, что Земля имеет форму шара. Если выразиться точнее, то у планеты форма эллипсоида вращения на малой оси, а еще точнее (учитывая разную сплюснутость у полюсов) - геоида. Правда, сторонники плоской Земли не верят в доказательства земной шарообразности, но их и не переубедить. Но вот кто конкретно доказал, что Земля круглая известно далеко не всем...
С железобетонной уверенностью можно утверждать, что экспедиция под управлением Фернана Магеллана, совершив кругосветное плавание, абсолютно точно доказала, что наша планета имеет форму схожую с шаром. Увы, сам великий мореплаватель не дожил до возвращения в Европу. Однако и до этого плавания еще в античном мире была доказана шарообразность нашей планеты, причем шли ученые к этому поступательно.
В том что Земля имеет шарообразную форму был убежден величайший философ Древней Греции Платон (поскольку шар это идеальная форма), но доказать свои взгляды он так и не смог. А вот его ученик Аристотель пытался это сделать и достиг определенного успеха. Основных доказательств Аристотель приводил три, но, все они были скорее логическими, нежели строго научными.
Сами доказательства Аристотеля следующие:
1. С перемещением на север Полярная звезда становится все выше над горизонтом. Причем на юге можно увидеть звезды, которые никогда не видны на севере. Это возможно только в случае шарообразности Земли, если бы она была плоская, то все светила были бы видны везде одновременно на одной и той же высоте;
2. Созвездия на экваторе находятся высоко;
3. Если посмотреть на Луну во время ее затмения, то тень отбрасываемая Землей на это небесное тело всегда имеет круглую форму.
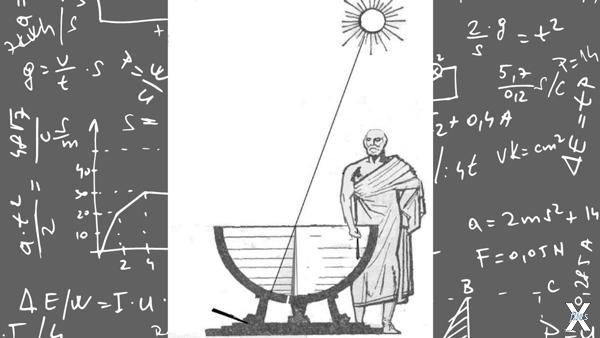
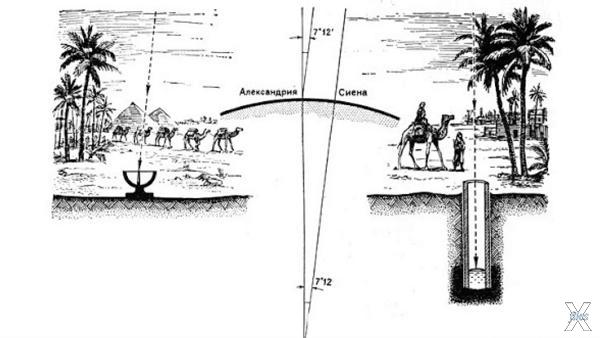
Полностью научно обоснованное доказательство шарообразности Земли с конкретными расчетами параметров произвел ученый из Александрии Эратосфен примерно в 240 году до Рождества Христова. Ему рассказывали, что в городе Сиена, расположенном на 5 000 стадий южнее на том же меридиане что и Александрия, в день летнего солнцестояния тень человека смотрящего в глубокий колодец закрывает в нем солнечное отражение. Проще говоря, в этот день предметы не отбрасывают тени, когда Солнце находится в зените.
А дальше в дело вступили простейшие измерения и законы геометрии. Фактически, единственным, что нужно было узнать Эратосфену, так это длину тени от некоего единичного измерительного шеста отбрасываемую им в день летнего солнцестояния в момент нахождения Солнца в зените. Вполне схожий эксперимент поставил дворецкий Брайтон в рассказе сэра Артура Конан Дойла «Обряд дома Месгрейвов».
Это измерение было проведено с помощью скафиса (чашеобразных солнечных часов, разделенных ученым на градусы) и мерного шеста гномона, с отверстием на конце, чтобы по яркой точке точнее проводить измерения тени.
Оказалось, что угол между Солнцем в зените в день летнего солнцестояния в Александрии составляет примерно 7,2 градуса или 1/50 часть круга. А вот в Сиене он в это время равен 0! Теперь можно было вычислить чему равна окружность земного шара.
Оставалось посчитать несложную пропорцию:
Это и есть окружность нашей планеты. К сожалению, перевести используемые Эратосфеном стадии в привычные нам километры сейчас практически невозможно, поскольку неизвестно, каким именно стадием пользовался в своих расчетах древнегреческий ученый. В то время использовались стадии, которые нынче составляют 157,2 м, 172,5 м (египетский), 178 м (греческий) и 209,4 м (системы фараонов) соответственно. Были и другие стадии, в том числе олимпийский равный 192,27 м. Так что длина земной окружности по Эратосфену находится в рамках 40 000- 50 000 км.
На этом древнегреческий ученый не остановился. Он знал формулу связи радиуса окружности с ее длиной:
Прошло еще примерно лет 200 и Страбон привел свое логическое доказательство шарообразности Земли — он первый обратил внимание на то, что нижняя часть корабля находящегося на линии горизонта не видна. А это возможно только из-за кривизны поверхности нашей планеты. Кстати, именно кривизна Земли ограничивает расстояние артиллерийского боя кораблей цифрой около 20 км при прямой видимости (немногим больше 100 кабельтовых).
С железобетонной уверенностью можно утверждать, что экспедиция под управлением Фернана Магеллана, совершив кругосветное плавание, абсолютно точно доказала, что наша планета имеет форму схожую с шаром. Увы, сам великий мореплаватель не дожил до возвращения в Европу. Однако и до этого плавания еще в античном мире была доказана шарообразность нашей планеты, причем шли ученые к этому поступательно.
В том что Земля имеет шарообразную форму был убежден величайший философ Древней Греции Платон (поскольку шар это идеальная форма), но доказать свои взгляды он так и не смог. А вот его ученик Аристотель пытался это сделать и достиг определенного успеха. Основных доказательств Аристотель приводил три, но, все они были скорее логическими, нежели строго научными.
Сами доказательства Аристотеля следующие:
1. С перемещением на север Полярная звезда становится все выше над горизонтом. Причем на юге можно увидеть звезды, которые никогда не видны на севере. Это возможно только в случае шарообразности Земли, если бы она была плоская, то все светила были бы видны везде одновременно на одной и той же высоте;
2. Созвездия на экваторе находятся высоко;
3. Если посмотреть на Луну во время ее затмения, то тень отбрасываемая Землей на это небесное тело всегда имеет круглую форму.
Полностью научно обоснованное доказательство шарообразности Земли с конкретными расчетами параметров произвел ученый из Александрии Эратосфен примерно в 240 году до Рождества Христова. Ему рассказывали, что в городе Сиена, расположенном на 5 000 стадий южнее на том же меридиане что и Александрия, в день летнего солнцестояния тень человека смотрящего в глубокий колодец закрывает в нем солнечное отражение. Проще говоря, в этот день предметы не отбрасывают тени, когда Солнце находится в зените.
А дальше в дело вступили простейшие измерения и законы геометрии. Фактически, единственным, что нужно было узнать Эратосфену, так это длину тени от некоего единичного измерительного шеста отбрасываемую им в день летнего солнцестояния в момент нахождения Солнца в зените. Вполне схожий эксперимент поставил дворецкий Брайтон в рассказе сэра Артура Конан Дойла «Обряд дома Месгрейвов».
Это измерение было проведено с помощью скафиса (чашеобразных солнечных часов, разделенных ученым на градусы) и мерного шеста гномона, с отверстием на конце, чтобы по яркой точке точнее проводить измерения тени.
Оказалось, что угол между Солнцем в зените в день летнего солнцестояния в Александрии составляет примерно 7,2 градуса или 1/50 часть круга. А вот в Сиене он в это время равен 0! Теперь можно было вычислить чему равна окружность земного шара.
Оставалось посчитать несложную пропорцию:
7,2/360 = 5 000/ х
Отсюда следует, х = 360*5 000/7,2 = 50*5000 =250 000 стадий.
Это и есть окружность нашей планеты. К сожалению, перевести используемые Эратосфеном стадии в привычные нам километры сейчас практически невозможно, поскольку неизвестно, каким именно стадием пользовался в своих расчетах древнегреческий ученый. В то время использовались стадии, которые нынче составляют 157,2 м, 172,5 м (египетский), 178 м (греческий) и 209,4 м (системы фараонов) соответственно. Были и другие стадии, в том числе олимпийский равный 192,27 м. Так что длина земной окружности по Эратосфену находится в рамках 40 000- 50 000 км.
Согласно нынешним данным длина земной окружности по меридиану (именно ее измерял Эратосфен) равна примерно 40 008, а по экватору около 40 075 км.
На этом древнегреческий ученый не остановился. Он знал формулу связи радиуса окружности с ее длиной:
L = 2 π*R где π= 3,14, а потому смог рассчитать радиус нашей планеты.
R = L/2π = 250 000/2*3,14 = 39 808 стадий.
При использовании стадия в 157,2 м получается 6302 км, при том что усредненный радиус Земли равен 6371 км.
Прошло еще примерно лет 200 и Страбон привел свое логическое доказательство шарообразности Земли — он первый обратил внимание на то, что нижняя часть корабля находящегося на линии горизонта не видна. А это возможно только из-за кривизны поверхности нашей планеты. Кстати, именно кривизна Земли ограничивает расстояние артиллерийского боя кораблей цифрой около 20 км при прямой видимости (немногим больше 100 кабельтовых).
Опубликовано 16 октября 2020
Комментариев 0 | Прочтений 1408
Ещё по теме...
Добавить комментарий
Из новостей
Периодические издания
Информационная рассылка: